“天地有正气，杂然赋流形 – 文天祥”

I am a Ph.D. student affiliated with Multimedia and Human Understanding Group (MHUG) at University of Trento, Italy, advised by Prof. Nicu Sebe. Before my Ph.D. studies, I received a B.A. degree in logistics management from Shandong University, Jinan, China, and an M.S. degree in computer science and technology from Jiangnan University, Wuxi, China, under the supervision of Prof. Xiao-Jun Wu and Prof. Josef Kittler.

My research lies in the intersection of machine learning and differential geometry, such as geometric deep learning. I also co-supervise several students with Rui Wang. I am always open for collaboration. If you are interested in my research, please drop me an email.

I am building a GitHub repo, Awesome-Riemannian-Deep-Learning, containing resources on deep learning over Riemannian spaces. 🚀

🌟 News

📝 Selected Publications

(† denotes the corresponding author)

ICLR 2025

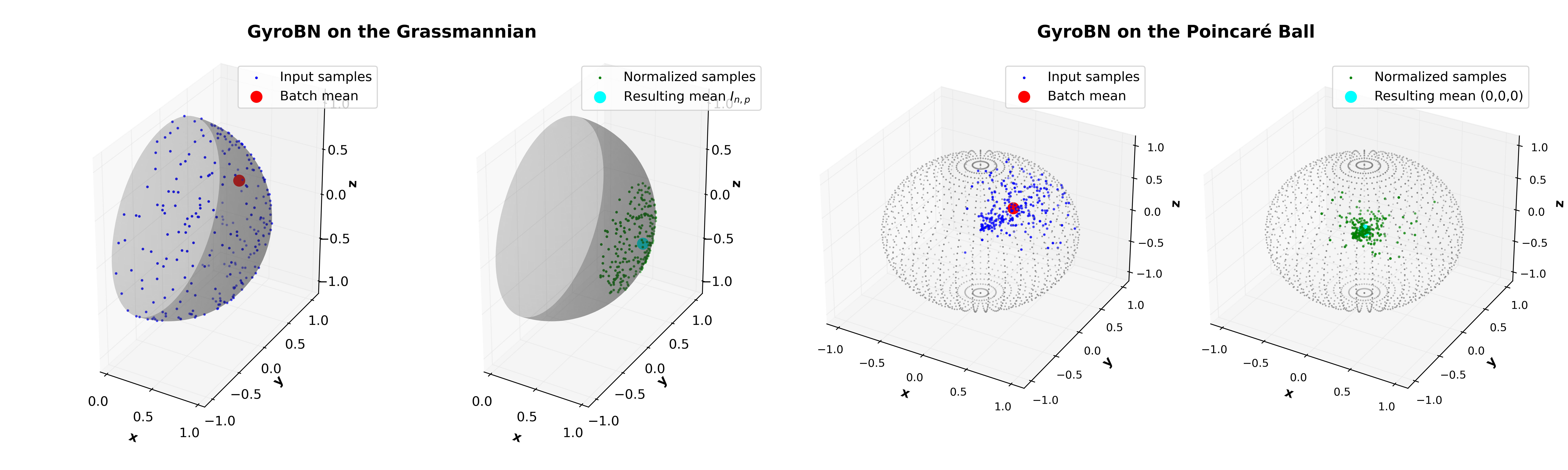
Gyrogroup Batch Normalization
Ziheng Chen, Yue Song, Xiaojun Wu, Nicu Sebe. [Code]

• Proposes pseudo-reductive gyrogroups, a relaxed structure of gyrogroups, with complete theoretical analyses.
• Establishes the conditions for theoretical control over sample statistics in Riemannian batch normalization over gyrogroups, i.e., pseudo-reduction and gyroisometric gyrations.
• Introduces a GyroBN framework for Riemannian Batch Normalization over gyrogroups, applicable to various geometries.
• Manifests GyroBN on the Grassmannian and hyperbolic spaces.

ICLR 2025

Understanding Matrix Function Normalizations in Covariance Pooling through the Lens of Riemannian Geometry
Ziheng Chen, Yue Song, Xiaojun Wu, Gaowen Liu, Nicu Sebe. [Code]

• Explains the working mechanism of matrix functions in Global Covariance Pooling from the perspectives of tangent and Riemannian classifiers, and finally claims that the rationality of matrix functions should be attributed to the Riemannian classifiers they implicitly respect.
• Validates the theoretical argument on the ImageNet and three FGVC datasets through comprehensive experiments.

NeurIPS 2024

RMLR: Extending Multinomial Logistic Regression into General Geometries
Ziheng Chen, Yue Song, Rui Wang, Xiaojun Wu, Nicu Sebe. [Code]

• Extends our flat SPD MLR (CVPR24) into Riemannian MLR over general geometries.
• Proposes five families of SPD MLRs based on different geometries of the SPD manifold.
• Proposes a novel Lie MLR for deep neural networks on rotation matrices.

ICLR 2024

A Lie Group Approach to Riemannian Batch Normalization
Ziheng Chen, Yue Song, Yunmei Liu, Nicu Sebe. [Code]

• Propose a Riemannian batch normalization (LieBN) framework over general Lie groups, with controllable first- and second-order statistical moments.
• Manifests specific LieBN layers on SPD manifolds under three deformed Lie groups as well as the Lie group of rotation matrices.

CVPR 2024

Riemannian Multinomial Logistics Regression for SPD Neural Networks
Ziheng Chen, Yue Song, Gaowen Liu, Ramana Rao Kompella, Xiaojun Wu, Nicu Sebe. [Code]

• Extends the Euclidean Multinomial Logistic Regression (MLR) to the SPD manifold under flat Riemannian metrics.
• Manifests the framework on the Log-Euclidean (LE) and Log-Cholesky (LC) metrics.
• Provides the first intrinsic explanation for the widely used LogEig classifier.

Arxiv 2024

Product Geometries on Cholesky Manifolds with Applications to SPD Manifolds
Ziheng Chen, Yue Song, Xiao-Jun Wu, Nicu Sebe. [Code]

• Identifies the underlying product structure in the existing Cholesky metric.
• Introduces two novel Riemannian metrics on the Cholesky manifold, along with a comprehensive analysis of their geometric properties.
• Proposes two numerically stable Riemannian metrics on the SPD manifold, with a detailed analysis of their geometric properties.

TIP 2024

Adaptive Log-Euclidean Metrics for SPD Matrix Learning
Ziheng Chen, Yue Song, Tianyang Xu, Zhiwu Huang, Xiao-Jun Wu, and Nicu Sebe. [Code]

• Proposes a general framework for pullback metrics over the SPD manifold from the Euclidean space.
• Extends the existing Log-Euclidean Metric (LEM) into ALEM.

Preprints

• Arxiv 2024 Product Geometries on Cholesky Manifolds with Applications to SPD Manifolds, Ziheng Chen, Yue Song, Xiao-Jun Wu, Nicu Sebe. [Code]

Conferences

• CVPR 2025 Learning to Normalize on the SPD Manifold under Bures-Wasserstein Geometry, Rui Wang, Shaocheng Jin, Ziheng Chen^†, Xiaoqing Luo, Xiao-Jun Wu. [Code]

• ICLR 2025 Gyrogroup Batch Normalization, Ziheng Chen, Yue Song, Xiao-Jun Wu, Nicu Sebe. [Code] [Slides] [Poster] [Video]

• ICLR 2025 Understanding Matrix Function Normalizations in Covariance Pooling through the Lens of Riemannian Geometry, Ziheng Chen, Yue Song, Xiao-Jun Wu, Gaowen Liu, Nicu Sebe. [Code] [Slides] [Poster] [Video]
• NeurIPS 2024 RMLR: Extending Multinomial Logistic Regression into General Geometries, Ziheng Chen, Yue Song, Rui Wang, Xiao-Jun Wu, Nicu Sebe. [Code] [Slides] [Poster] [Video]

• IJCAI 2024 A Grassmannian Manifold Self-Attention Network for Signal Classification, Rui Wang, Chen Hu, Ziheng Chen^†, Xiao-Jun Wu^†, Xiaoning Song. [Code]

• CVPR 2024 Riemannian Multinomial Logistics Regression for SPD Neural Networks, Ziheng Chen, Yue Song, Gaowen Liu, Ramana Rao Kompella, Xiao-Jun Wu, Nicu Sebe. [Code] [Slides] [Poster] [Video]

• ICLR 2024 A Lie Group Approach to Riemannian Batch Normalization, Ziheng Chen, Yue Song, Yunmei Liu, Nicu Sebe. [Code] [Slides] [Poster] [Video]
• AAAI 2023 Riemannian Local Mechanism for SPD Neural Networks, Ziheng Chen, Tianyang Xu, Xiao-Jun Wu, Rui Wang, Zhiwu Huang, Josef Kittler. [Code] [Slides] [Poster]

Journals

• TNNLS 2025 Learning a Better SPD Network for Signal Classification: A Riemannian Batch Normalization Method, Rui Wang, Shaocheng Jin, Zhenyu Cai, Ziheng Chen^†, Xiao-Jun Wu^†, Josef, Kittler.

• TIM 2025 Structural Topology Refinement Network for Skeleton-Based Action Recognition, Rui Wang, Jiayao Jin, Ziheng Chen^†, Cong Wu^†, Xiao-Jun Wu, Nicu Sebe [Code]
• TIP 2024 Adaptive Log-Euclidean Metrics for SPD Matrix Learning, Ziheng Chen, Yue Song, Tianyang Xu, Zhiwu Huang, Xiao-Jun Wu, Nicu Sebe. [Code]
• TNNLS 2024 SPD Manifold Deep Metric Learning for Image Set Classification, Rui Wang, Xiao-Jun Wu, Ziheng Chen, Cong Hu, Josef Kittler. [Code]
• TBD 2021 Hybrid Riemannian Graph-Embedding Metric Learning for Image Set Classification, Ziheng Chen, Tianyang Xu, Xiao-Jun Wu, Rui Wang, Josef Kittler. [Code]

🎖 Honors and Awards

• 2025.07: ELSA Mobility Grant (3,000 EUR)
• 2025.05: ELIAS Mobility Grant (2,400 EUR)
• 2024.06: Awarded 80,000 GPU hours by CINECA under the ISCRA initiative
• 2023.12: Excellent Master’s Thesis of Jiangsu Association of Artificial Intelligence (Only 7 awards granted in Jiangsu Province; 江苏省人工智能学会优秀硕士论文，全省仅 7 篇)

💬 Invited Talks

• 2025.06: Extending Normalization into Riemannian Manifolds. Jiangnan University.
• 2025.03: Riemannian Deep Learning: Normalization and Classification. University of Alberta. [Slides]
• 2024.03: Naïve Riemannian Geometry: A One Hour Tour. Jiangnan University (internal talk).

📖 Courses

To obtain basic foundations for my research, I have self-studied several math courses, most of which were done during my master studies:

• Mathematical Analysis I, II, III, Real Analysis, Complex Analysis, Functional Analysis;
• Advanced Algebra I, II, Abstract Algebra I;
• Topology, Differential Geometry, Differential Manifolds, Riemannian Geometry;
• Differential Equations, Convex Optimization, Numerical Optimization…

💻 Personal Channels

• Differential Equations (1k+ viewers)
• Topology (2k+ viewers)
• Differential Geometry (1w+ viewers)
• Riemannian Geometry (2k+ viewers)
• Measure Theory